Necessary and sufficient condition

In logic, the words necessity and sufficiency refer to the implicational relationships between statements. The assertion that one statement is a necessary and sufficient condition of another means that the former statement is true if and only if the latter is true.

Contents

Definitions

A necessary condition of a statement must be satisfied for the statement to be true. In formal terms, a statement N is a necessary condition of a statement S if S implies N (S 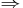\Rightarrow N).

A sufficient condition is one that, if satisfied, assures the statement's truth. In formal terms, a statement S is a sufficient condition of a statement N if S implies N (S 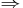\Rightarrow N).

Necessary conditions

The assertion that P is necessary for Q is colloquially equivalent to "Q cannot be true unless P is true," or "if P is false then Q is false." By contraposition, this is the same thing as "whenever Q is true, so is P". The logical relation between them is expressed as "If Q then P" and denoted "Q 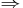\Rightarrow P" (Q implies P), and may also be expressed as any of "P, if Q"; "P whenever Q"; and "P when Q." One often finds, in mathematical prose for instance, several necessary conditions that, taken together, constitute a sufficient condition, as shown in Example 5.

Example 1: In order for it to be true that "John is a bachelor," it is necessary that it be also true that he is
  1. unmarried
  2. male
  3. adult
since to state "John is a bachelor" implies John has each of those three additional predicates.
Example 2: For the whole numbers greater than two, being odd is necessary to being prime, since two is the only whole number that is both even and prime.
Example 3: Consider thunder, in the technical sense, the acoustic quality demonstrated by the shock wave that inevitably results from any lightning bolt in the atmosphere. It may fairly be said that thunder is necessary for lightning, since lightning cannot occur without thunder, too, occurring. That is, if lightning does occur, then there is thunder.
Example 4: Being at least 30 years old is necessary of serving in the U.S. Senate. If you are under 30 years old then it is impossible for you to be a senator. That is, if you are a senator, it follows that you are at least 30 years old.
Example 5: In algebra, in order for some set S together with an operation \star to form a group, it is necessary that \star be associative. It is also necessary that S include a special element e such that for every x in S it is the case that e \star x and x \star e both equal x. It is also necessary that for every x in S there exist a corresponding element x” such that both x \star x” and x” \star x equal the special element e. None of these three necessary conditions by itself is sufficient, but the conjunction of the three is.

Sufficient conditions

To say that P is sufficient for Q is to say that, in and of itself, knowing P to be true is adequate grounds to conclude that Q is true. (It is to say, at the same time, that knowing P not to be true does not, in and of itself, provide adequate grounds to conclude that Q is not true, either.) The logical relation is expressed as "If P then Q" or "P 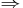\Rightarrow Q," and may also be expressed as "P implies Q." Several sufficient conditions may, taken together, constitute a single necessary condition, as illustrated in example 5.

Example 1: Stating that "John is a bachelor" implies that John is male. So knowing that it is true that John is a bachelor is sufficient to know that he is a male.
Example 2: A number's being divisible by 4 is sufficient (but not necessary) for its being even, but being divisible by 2 is both sufficient and necessary.
Example 3: An occurrence of thunder is a sufficient condition for the occurrence of lightning in the sense that hearing thunder, and unambiguously recognizing it as such, justifies concluding that there has been a lightning bolt.
Example 4: A U.S. president's signing a bill that Congress passed is sufficient to make the bill law. Note that the case whereby the president did not sign the bill, e.g. through exercising a presidential veto, does not mean that the bill has not become law (it could still have become law through a congressional override).
Example 5: That the center of a playing card should be marked with a single large spade (♠) is sufficient for the card to be an ace. Three other sufficient conditions are that the center of the card be marked with a diamond (♦), heart (♥), or club (♣), respectively. None of these conditions is necessary to the card's being an ace, but their disjunction is, since no card can be an ace without fulfilling at least (in fact, exactly) one of the conditions.

Relationship between necessity and sufficiency

A condition can be either necessary or sufficient without being the other. For instance, being a mammal (P) is necessary but not sufficient to being human (Q), and that a number q is rational (P) is sufficient but not necessary to q‘s being a real number (Q) (since there are real numbers that are not rational).

A condition can be both necessary and sufficient. For example, at present, "today is the Fourth of July" is a necessary and sufficient condition for "today is Independence Day in the United States." Similarly, a necessary and sufficient condition for invertibility of a matrix M is that M has a nonzero determinant.

Mathematically speaking, necessity and sufficiency are dual to one another. For any statements P and Q, the assertion that “P is necessary for Q” is equivalent to the assertion that “Q is sufficient for P.” Another facet of this duality is that, as illustrated above, conjunctions of necessary conditions may achieve sufficiency, while disjunctions of sufficient conditions may achieve necessity. For a third facet, identify every mathematical predicate P with the set S(P) of objects for which P holds true; then asserting the necessity of P for Q is equivalent to claiming that S(P) is a superset of S(Q), while asserting the sufficiency of P for Q is equivalent to claiming that S(P) is a subset of S(Q).

Simultaneous necessity and sufficiency

See also: Material equivalence

To say that P is necessary and sufficient for Q is to say two things, that P is necessary for Q and that P is sufficient for Q. Of course, it may instead be understood to say a different two things, namely that each of P and Q is necessary for the other. And it may be understood in a third equivalent way: as saying that each is sufficient for the other. One may summarize any—and thus all—of these cases by the statement "P if and only if Q," which is denoted by P \Leftrightarrow Q.

For example, in graph theory a graph G is called bipartite if it is possible to assign to each of its vertices the color black or white in such a way that every edge of G has one endpoint of each color. And for any graph to be bipartite, it is a necessary and sufficient condition that it contain no odd-length cycles. Thus, discovering whether a graph has any odd cycles tells one whether it is bipartite and vice versa. A philosopher[1] might characterize this state of affairs thus: "Although the concepts of bipartiteness and absence of odd cycles differ in intension, they have identical extension.[2]

See also

Argument forms involving necessary and sufficient conditions

Valid forms of argument

Invalid forms of argument (i.e. fallacies)

References

  1. ^ Stanford University primer, 2006
  2. ^ "Meanings, in this sense, are often called intensions, and things designated, extensions. Contexts in which extension is all that matters are, naturally, called extensional, while contexts in which extension is not enough are intensional. Mathematics is typically extensional throughout." Stanford University primer, 2006

External links